算數平均數：也就是平常我們常用的平均數，將資料全部相加後除以資料個數。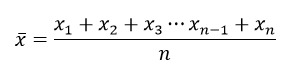

缺點：易受到離群值（極端數）影響
使用時機：計算平均月支出
例子：
小明1月支出100元、2月支出1000元、3月支出700元
這三個月平均月支出為 (100+1000+700)/3=600元

幾何平均數：
1.跟算術平均數比起來，較不會受到離群值影響
2.如果變量值有負值，計算出的幾何平均數就會成為負數或虛數
3.它僅適用於具有等比或近似等比關係的數據
4.幾何平均數的對數是各變量值對數的算術平均數。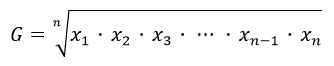

缺點：不適用資料中有0的、負數
使用時機：計算平均利率、年成長率、合格率
例子：
第一年公司營收成長率為2.5倍、第二年為3.5倍、第三年為0.8倍，求該公司平均成長率？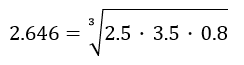

n=3年

調和平均數：
1、調和平均數易受極端值的影響，且受極小值的影響比受極大值的影響更大
2、只要有一個變數值為零，就不能計算調和平均數
3、當組距數列有開口組時，其組中值即使按相鄰組距計算了，假定性也很大，這時，調和平均數的代表性就很不可靠
4、調和平均數應用的範圍較小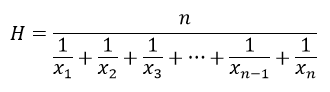

缺點：不適用資料有0的、極易受離群值影響
使用時機：計算速度、電阻平均數
例子：
小名從公司到家裡距離1公里，走路時速6km，回到家後又從家裡去朋友家，距離也是1公里，騎腳踏車車時速12km，求小名的調和平均數？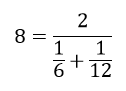

n=2(公司到家裡1公里+家裡到朋友家1公里=2公里)
調和平均數：8km/h
算術平均數：9km/h

使用相同資料計算出來的數字：
算術平均數 ≥ 幾何平均數 ≥ 調和平均數